PROBLEM FORMULATION: Early on in my development of inversion, I modeled the interior structure of inverting airfoils off of the classical airfoil rib and ram air kite bridle supports. However, inflated morphing airfoils act very differently from rigid ones when introduced to concentrated pressure distributions in flight. I sought to 1) numerically predict what shape the airfoil would inflate given constrained interior supports, 2) change that support arrangement for inflation to a desired airfoil shape, and 3) determine how the airfoil surfaces would deform under expected aerodynamic loads.

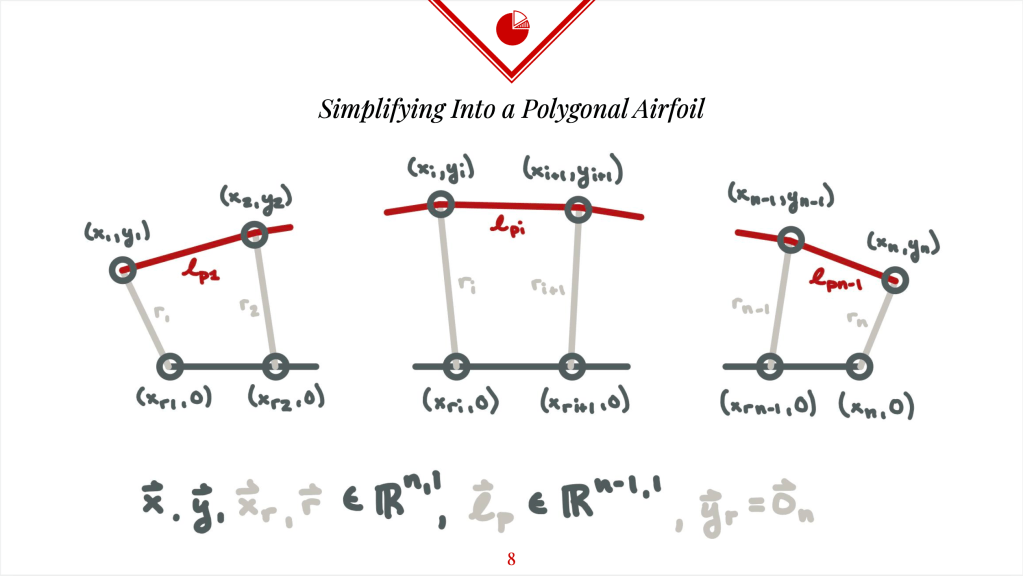
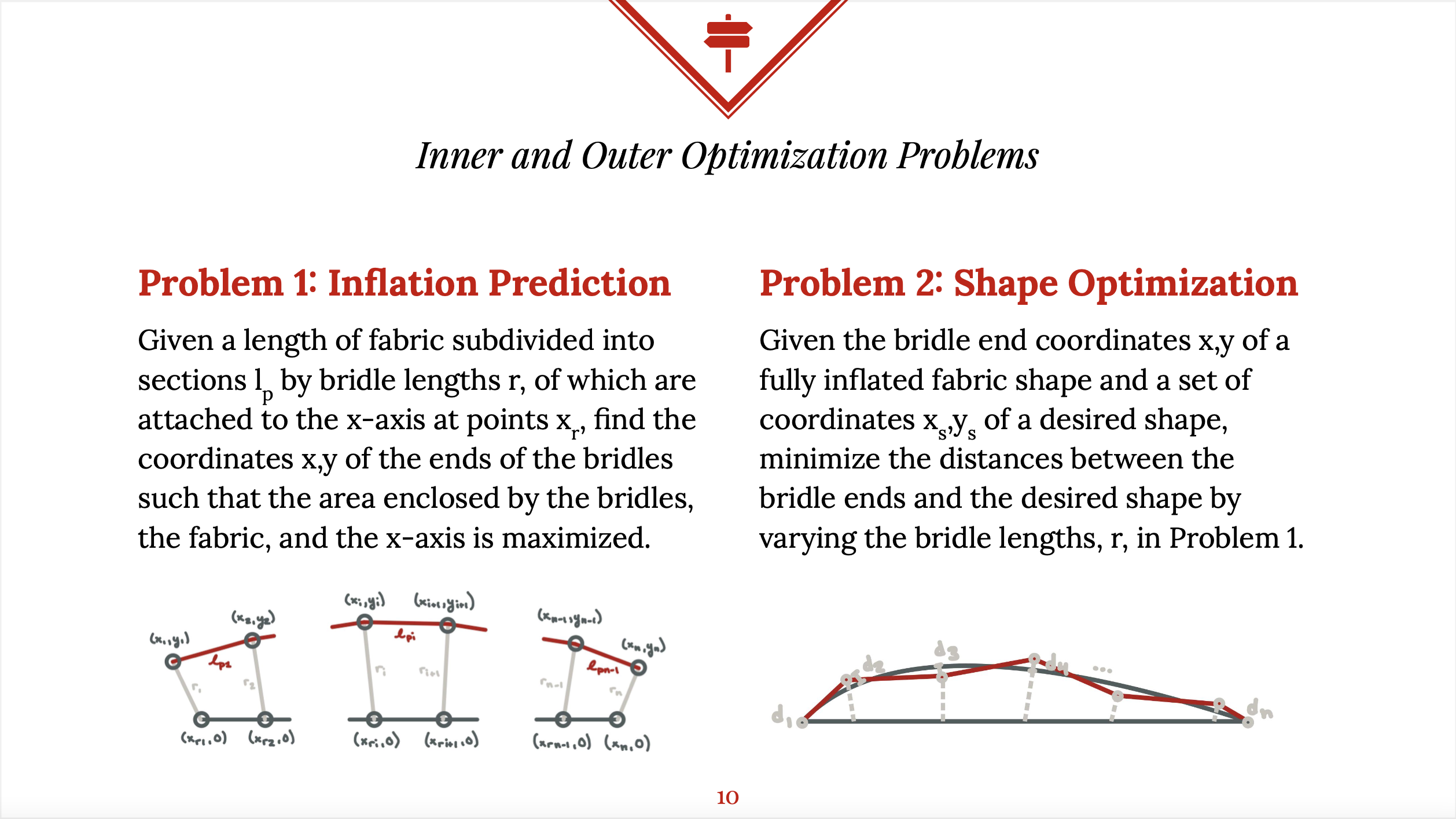
QCQP NON-CONVEXITY: With guidance from Professor Ganapati of Swarthmore College, I framed this problem as a simplified polygonal optimization question, where the objective function was to minimize error between an input shape and the maximized airfoil region allowed by support constraints. Ultimately, I proved that this problem was a non-convex Quadratically Constrained Quadratic Program (QCQP), and that the inflated airfoil shape would be sensitive to external loading. As such, I changed my airfoil supports to a current sheet arrangement. (Images chosen from an initial optimization problem proposal sent to Professor Ganapati in March 2022, also from my presentation of this material to an engineering optimization class.)

DESCENDING FLIGHT THEORY: I am also currently investigating a derivation for the theoretical maximum efficiency increase that inverting airfoils can offer over reeled AWE kites. Basing my setup on the classical Benz equation for maximum wind turbine efficiency and the equivalent derivation by Loyd for crosswind kite power, I hope to find an optimal descending flight path to minimize time and energy expended by the kite.